Contents
Mergulhos Aparentes#
Na extração da atitude de planos com bússolas, via de regra o mergulho de uma superfície inclinada é medido ortogonalmente à direção da estrutura. Caso essa premissa seja atendida, estaremos medindo o mergulho verdadeiro daquela superfície.
No entanto, não são raras as situações em que não seja possível medir diretamente o mergulho verdadeiro de uma superfície geológica. Em muitos casos, os planos das camadas podem não estar apropriadamente expostos, mas apenas os seus traços.
Nota
Traço é a linha formada pela interseção de duas superfícies.
É muito comum que exposições de rochas (como em falésias, cortes de estrada, paredes de galerias etc.) estejam orientadas em quaisquer ângulos relativamente à direção das camadas. Se essas exposições não forem perpendiculares à direção da superfície geólogica de interesse, então serão medidos mergulhos aparentes dessas superfícies nas exposições. É importante notar que para uma dada superfície, os mergulhos aparentes medidos em diferentes cortes sempre serão menores que o respectivo mergulho verdadeiro.
A relação entre o mergulho aparente e o mergulho verdadeiro de uma camada depende da direção do corte vertical arbitrário que intercepta as camadas. Ou seja, a razão entre o mergulho aparente e o mergulho verdadeiro é proporcional à obliquidade entre a seção em que o mergulho aparente é medido e:
a seção em que o mergulho verdadeiro é medido;
ou a direção da respectiva superfície geológica.
Existem várias formas de determinar o mergulho verdadeiro de uma superfície geológica, dados um ou dois mergulhos aparentes. Nesse capítulo, serão utilizadas projeções ortográficas.
Importante!
Sempre antes de se tentar resolver os problemas, inicialmente é importante construir uma visão tridimensional dele, lançando mão das informações dadas (Figura 1a).
Desenhe de forma esquemática a linha de direção da estrutura geológica (um contato, por exemplo), bem como o traço do corte vertical no qual deve ser medido ou determinado o mergulho verdadeiro da estrutura. Lembre que essas duas linhas perfazem um ângulo reto entre si. Desenhe na mesma figura o traço do corte ou perfil no qual o mergulho aparente é observado, medido ou determinado. Esses três segmentos de retas deverão constituir as arestas de um triângulo retângulo, tal que o vértice que contém o ângulo reto seja formado entre a linha de direção e o corte do mergulho verdadeiro. Atente que esse triângulo retângulo é horizontal e, no campo, estaria contido no piso de um afloramento.
Nota
Esse desenho esquemático ajudará a visualizar em mapa de forma preliminar os dados do problema. Mesmo sendo esquemático, procure desenhar as três linhas de forma que estejam corretamente orientadas, ainda que aproximadamente, em relação ao norte verdadeiro. Somente passe para a resolução exata do problema estiver confiante de sua construção.
Lembre que o primeiro passo para solucionar um problema é entendê-lo!
Determinação do mergulho verdadeiro quando se conhece um mergulho aparente#
Inicialmente, abordaremos o caso em que queremos determinar o valor do mergulho verdadeiro (\(\delta\)) de uma superfície geológica, dado o valor de um mergulho aparente (\(\delta'\)). Além disso, também será necessária pelo menos uma das informações a seguir:
Os azimutes do traço do corte em que foi medido o mergulho aparente e do traço do corte em que foi medido o mergulho verdadeiro. A partir dessas informações, pode-se determinar o ângulo agudo (\(\alpha\)) formado entre essas duas linhas;
Os azimutes do traço do corte em que foi medido o mergulho aparente e da linha de direção da superfície geológica. A partir dessas informações, pode-se determinar o ângulo agudo (\(\beta\)) formado entre essas duas linhas;
Os azimutes do traço do corte em que foi medido o mergulho aparente, ou traço do corte em que foi medido o mergulho verdadeiro ou da linha de direção da superfície geológica e um dos ângulos \(\alpha\) ou \(\beta\).
Agora, siga o passo-a-passo seguinte para solucionar o problema:
Empregando as ferramentas apropriadas (esquadros, transferidor, compasso), desenhe em mapa a linha de direção e os traços dos cortes em que são identificados os mergulhos verdadeiro e aparente, de maneira que as três linhas correspondam às arestas do triângulo retângulo (Figura 1b) conforme esquematizado inicialmente. Esses segmentos de reta devem estar devidamente orientados em relação ao norte verdadeiro. Uma vez mais, identifique e anote corretamente os ângulos \(\alpha\) e \(\beta\) nos vértices do triângulo. Para auxiliar no entendimento dos passos seguintes, chame o vértice com o ângulo \(\alpha\) de \(\rm{A}\), o vértice com o ângulo \(\beta\) de \(\rm{B}\) e o vértice com o ângulo reto de \(\rm{O}\) (Figura 1b);
Nota
O segmento de reta \(\overline{\rm{OB}}\) corresponde à linha de direção da superfície geológica. O segmento de reta \(\overline{\rm{OA}}\) corresponde ao traço do corte vertical em que é medido (ou determinado) o mergulho verdadeiro, enquanto que o segmento de reta \(\overline{\rm{AB}}\) representa o traço do corte vertical em que é medido (ou determinado) o mergulho aparente (Figura 1b).
Importante!
Os segmentos de reta \(\overline{\rm{OA}}\) e \(\overline{\rm{AB}}\) servirão de linhas de dobradura por meio das quais os respectivos cortes serão rebatidos para a horizontal (Figura 1c), constituindo uma épura (Figura 1d). Quando isso acontecer, os ângulos verticais \(\delta\) e \(\delta'\) passarão a ser medidos na horizontal.
Trace uma reta com ângullo \(\delta'\) em relação ao segmento de reta \(\overline{\rm{AB}}\) e com origem no vértice \(\rm{A}\). Essa reta representa o traço da superfície (plano) geológica no corte vertical em que foi medido o mergulho aparente (Figura 1d);
Pelo vértice \(\rm{B}\), trace uma nova reta perpendicular ao segmento \(\overline{\rm{AB}}\) e que intercepte a reta traçada no passo 2. Chame o cruzamento dessas reta de \(\rm{P}\). O comprimento do segmento de reta \(\overline{\rm{BP}}\) é igual a \(\rm{d}\) (Figura 1d);
Pelo vértice \(\rm{O}\), trace uma reta ortogonal ao segmento \(\overline{\rm{OA}}\) e marque nele a distância \(\rm{d}\) determinada no passo 3. Chame esse ponto de \(\rm{Q}\) e trace um segmento de reta unindo os pontos \(\rm{A}\) e \(\rm{Q}\) (Figura 1e);
Pronto! O ângulo agudo formado entre os segmentos de reta \(\overline{\rm{OA}}\) e \(\overline{\rm{AQ}}\) é o mergulho verdadeiro da superfície geológica (Figura 1e).
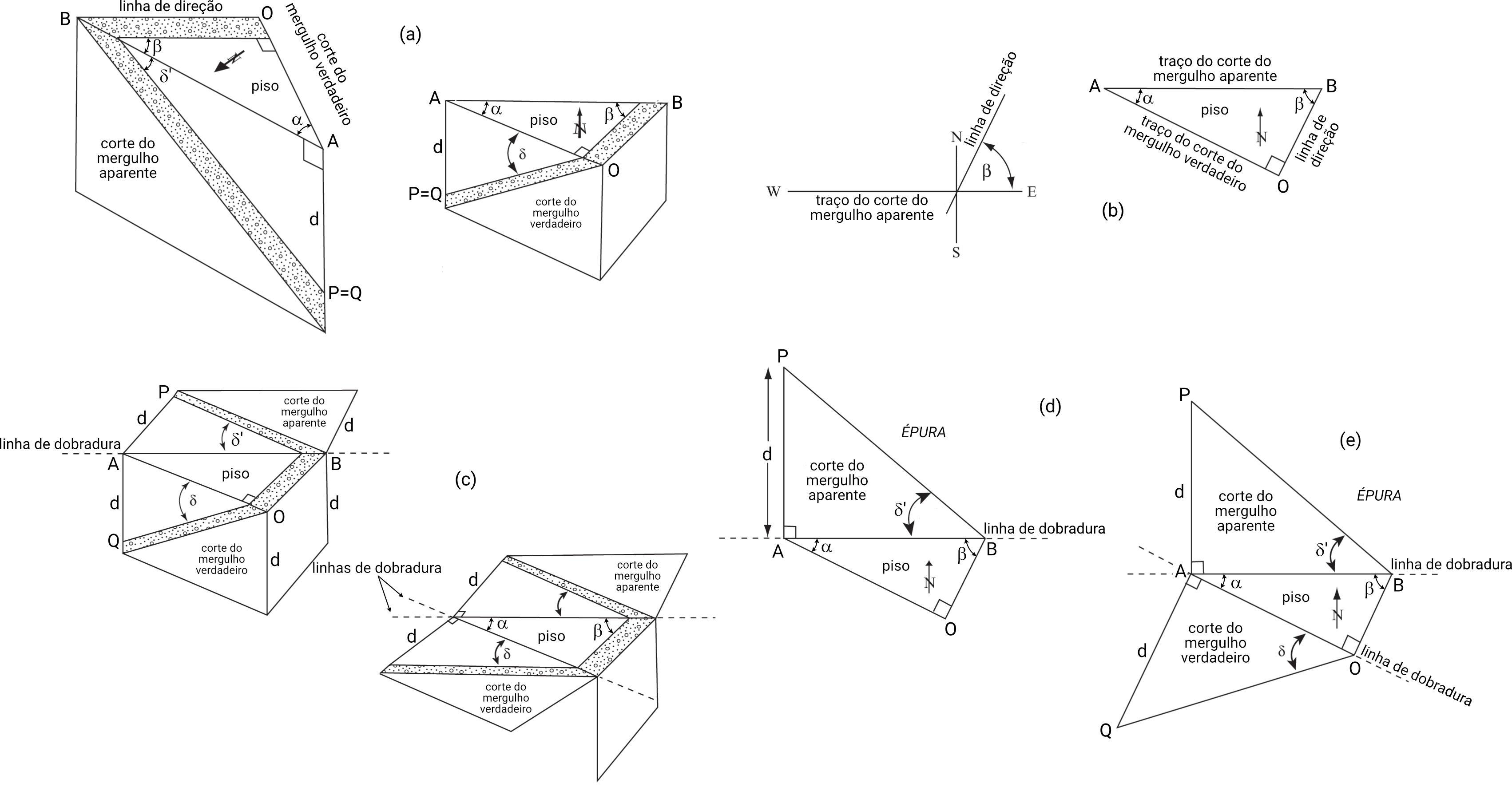
Fig. 1 A determinação do valor do mergulho verdadeiro (\(\delta\)) de uma superfície geológica pode ser solucionada pela utilização de projeções ortográficas. O primeiro passo para solução é entender o problema, passando pela contrução de uma visão tridimensional (a). Sempre que possível, procure construir mais de uma visão 3D, com diferentes visadas, a exemplo do exibido em (a). Em seguida, passe para a visão de mapa (b), de forma a projetar o piso do bloco diagrama no plano horizontal. Posicionar corretamente as retas relativas à linha de direção (segmento de reta \(\overline{\rm{OB}}\)), ao traço do corte em que pode ser medido o mergulho verdadeiro \(\delta\) ((segmento de reta \(\overline{\rm{OA}}\))) e ao traço do corte em que é medido o mergulho aparente \(\delta'\) (segmento de reta \(\overline{\rm{AB}}\)) é essencial para resolução do problema. Os segmentos de reta \(\overline{\rm{OA}}\) e \(\overline{\rm{AB}}\) funcionam como linhas de dobradura (c) em torno das quais os cortes que contêm \(\delta\) e \(\delta'\) serão rebatidos para o plano horizontal, constituindo uma épura (d, e) dos blocos diagramas exibidos em (a). Adaptado de [Rowland et al., 2007].#
Determinação do mergulho verdadeiro quando se conhecem dois mergulhos aparentes#
Também é possível determinar o mergulho verdadeiro de uma superfície sendo conhecidos dois mergulhos aparentes dessa superfície, medidos em dois cortes verticais não paralelos. Para esse caso, são necessárias as seguintes informações na solução do problema:
os valores dos mergulhos aparentes medidos em cada corte;
os azimutes de cada corte.
Uma vez mais, para facilitar a solução do problema e antes de utilizar o algoritmo seguinte, desenhe de forma esquemática as informações fornecidas, tal como nos problemas anteriores.
Para a solução do problema, chamaremos arbitrariamente os mergulhos aparentes de \(\delta'_{1}\) e \(\delta'_{2}\), medidos, respectivamente nos cortes 1 e 2 (Figura 2).
Trace, em mapa e de forma devidamente orientada em relação ao norte verdadeiro, as retas horizontais que representam no terreno os traços dos cortes 1 e 2. Chame o ponto de interseção dessas retas de \(\rm{O}\) (Figura 2b);
Tendo-se os traços dos cortes 1 e 2 como referência e a partir do ponto \(\rm{O}\), desenhe duas novas retas com ângulos iguais a \(\delta'_{1}\) e \(\delta'_{2}\) em relação a seus respectivos traços (Figura 2c). Essas novas retas correspondem aos traços da superfície (plano) geológica nos respectivos cortes verticais em que foram medidos os mergulhos aparentes;
Escolha um dos cortes (corte 1, por exemplo) e trace, em uma posição arbitrária, uma reta perpendicular ao traço horizontal do corte e que intercepte a respectiva reta correspondente ao traço da superfície geológica no corte vertical. O comprimento dessa nova reta é igual a \(\rm{d}\). Chame sua extremidade de \(\rm{P}\) (Figura 2d);
No corte remanescente, trace de forma análoga e em uma posição asbitrária uma reta perpendicular ao traço horizontal do corte e que também intercepte a respectiva reta correspondente ao traço da superfície geológica nesse corte. Tenha certeza que essa reta tenha comprimento maior que \(\rm{d}\). A partir do traço horizontal do corte, marque a distância \(\rm{d}\). Projete essa distância, até que ela intercepte o traço inclinado da superfície geológica. Chame o ponto de interseção de \(\rm{Q}\) (Figura 2d);
A projeção dos pontos \(\rm{P}\) e \(\rm{Q}\) na superfície horizontal são, respectivamente, os pontos \(\rm{X}\) e \(\rm{Y}\). Trace uma reta unindo os pontos \(\rm{X}\) e \(\rm{Y}\) (Figura 2e). Essa reta corresponde à linha de direção da superfície geológica.
Nota
Se desejar (ou se for necessário), meça o ângulo horário que essa linha perfaz com o norte verdadeiro. Esse ângulo corresonde ao azimute da linha de direção.
Passando pelo ponto \(\rm{O}\), trace uma reta perpencular à linha de direção (ou seja ao segmento de reta \(\overline{\rm{XY}}\)). Essa nova reta corresponde ao traço do corte em que será determinado o mergulho verdadeiro \(\delta\) da superfície gelógica. Para conveniência, chame a interseção da linha de direção com o corte em que será determinado o mergulho verdadeiro de \(\rm{R}\) (Figura 2f);
Importante!
Lembre que o mergulho verdadeiro sempre é medido em um corte vertical perpendicular à direção da superfície geológica.
Ao longo da linha de direção e a partir do ponto \(\rm{R}\), marque a distância \(\rm{d}\) e identifique esse ponto como \(\rm{T}\) (Figura 2f). Feito! O ângulo agudo formado entre os segmentos de reta \(\overline{\rm{OT}}\) e \(\overline{\rm{OR}}\) é o mergulho verdadeiro \(\delta\)!
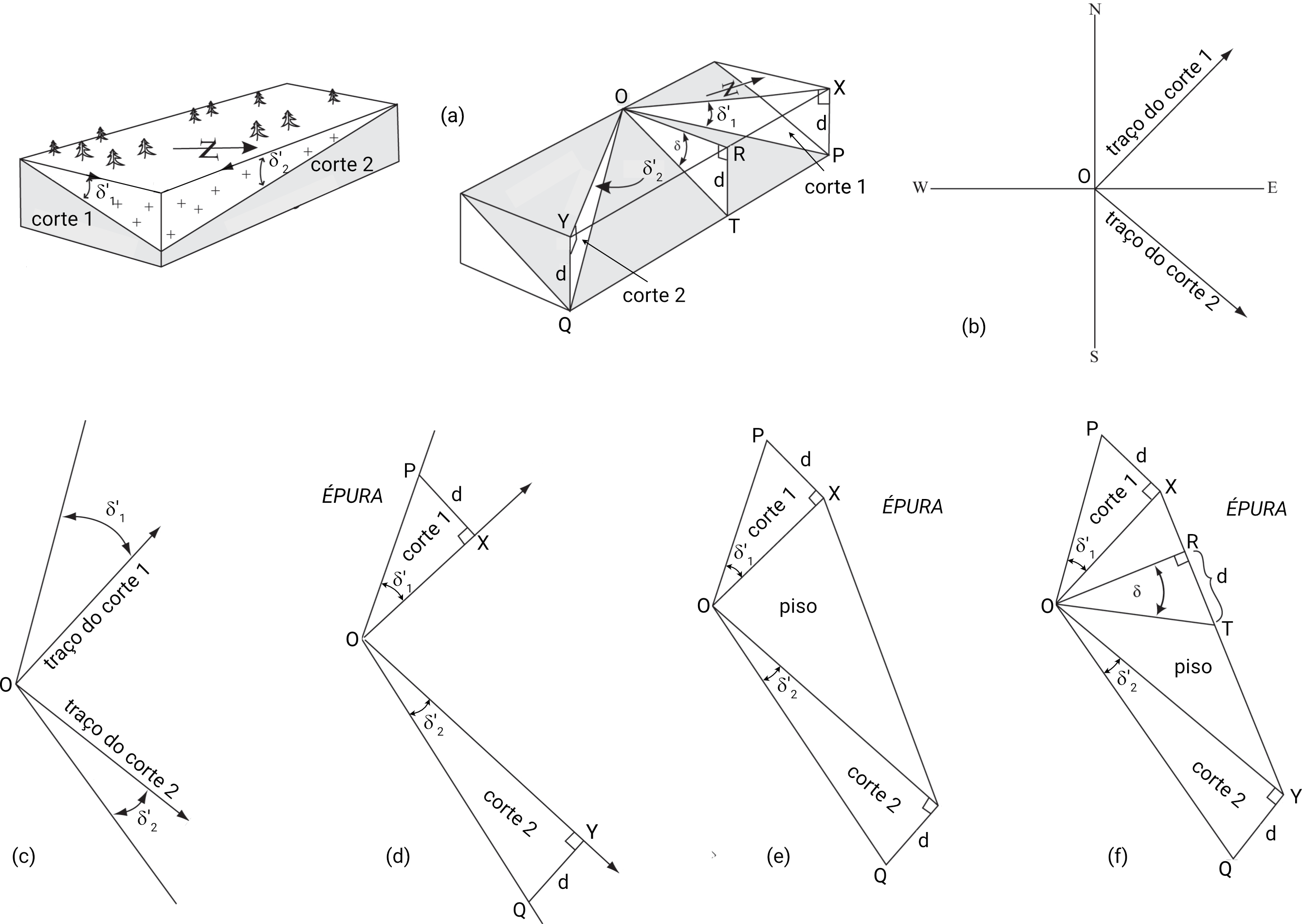
Fig. 2 Procedimento similar ode ser utilizado para se determinar o mergulho verdadeiro (\(\delta\)) de uma superfície geológica dados dois mergulhos aparentes (\(\delta'_{1}\) e \(\delta'_{2}\)) medidos em dois cortes não paralelos e oblíquos à direção da estrutura. Tal como no problema anterior, inicie construindo visualizações tridimensionais do problema, preferencialmente com mais de uma visada (a), em seguida passe para a construção 2D em mapa (b). Na projeção ortográfica, os mergulhos aparentes constituirão ângulos horizontais medidos a partir dos traços dos respectivos cortes em que foram medidos (c). As épuras são completas com a definição da distância \(\rm{d}\) em ambos os cortes (d) e o traçado da linha de direção da superfície geológica (e). Finalmente determina-se o mergulho verdadeiro com a marcação da distância \(\rm{d}\) ao longo da linha de direção (f). Adaptado de [Rowland et al., 2007].#

